Appendix F: Recombinational Stabilization (Theory)
Theory
|
|
EUGENE M. MCCARTHY, PHD GENETICS
Verne Grant was once the most prominent proponent of the idea that recombinational stabilization from interchromoset matings might be a frequent source of new types of plants. However, he ultimately concluded (e.g., Grant 1981: 269–270) that such events are rare in a natural setting. However, he appears to have left the effects of spatial and stochastic factors out of account. McCarthy et al. (1995), who conducted computer simulations of recombinational stabilization, did take such factors into account. These studies suggest that, in large hybrid populations, the occurrence of such events is almost inevitable over evolutionary time.
These simulations provided an important insight, that is, the production of such recombinant derivatives can be viewed as a single statistical event. In any one generation, in any one small portion of a hybrid zone, the complex series of matings leading to the emergence of a new recombinant derivative is an unlikely event. But from a statistical, stochastic perspective, each new generation is a new random trial. So is each new portion of the hybrid zone. So the statistics of recombinational stabilization are those of a random trial repeated a huge number of times. Under such circumstances, as any statistician knows, the probability of a positive outcome approaches unity as the number of trials becomes very large. Somewhere, sometime enough individuals of the recombinant type happen to occur in the same vicinity and mate. As a result, more individuals of that type are present in that vicinity in the next generation, further increasing the probability that individuals of the recombinant type will mate and produce more of their own kind. This amplifying cycle results in the recombinant type getting established as a new form of life.
However, the results of these simulations published in McCarthy et al. (1995) have been misrepresented in recent publications. For example, Mavárez et al. (2006: 868) say, “Homoploid hybrid speciation [i.e., the production of a new stable recombinant derivative]—hybridization without change in chromosome number—is considered very rare. This has been explained by the theoretical prediction that reproductive isolation between hybrids and their parents is difficult to achieve.” In support of the second of these two quoted statements, they cite McCarthy et al. (1995), which does not contain or imply any "theoretical prediction" that supports this assertion. Indeed, in summarizing the results of our theoretical work on the subject we specifically stated (ibid: 509) our results indicate the stabilization of recombinant derivatives of interchromoset matings
"is a workable mode of evolution, not only in the laboratory but also in nature. So long as the sterility of the hybrids is not absolute, the potential exists for the rapid reassortment of entire chromosomes into novel combinations whenever the new combination is advantageous. In this way, natural selection is able to exploit the rich genetic variability of the typical hybrid zone."
Clearly, this is no prediction that such events are rare. Coyne and Orr (2006: 341) said our model (i.e., McCarthy et al. 1995) ignored most ecological aspects. This is unfortunate," they say,
"since, as Grant (1981: 251–253) emphasized, a new hybrid type might be partially or fully isolated from its parental species by 'external' or ecological factors. If a new hybrid genotype can, for instance, occupy a habitat in which the parental species are fairly unfit, its chances of survival increase."
This criticism neglects an important point—the stabilization of a new recombinant derivative from interchromoset matings relies on a type of isolation that is "internal." Such a derivative differs from its parents with respect to structural rearrangements. Therefore matings of derivative individuals with either of the parental types result in structurally heterozygous offspring. Such is the case in any environment, no matter what the ecological factors might be. This is why McCarthy et al. left ecological factors out of their model. We wished to evaluate whether processes of this sort could effectively produce stable derivatives even when they were not favored by an environmental advantage. Obviously, if the process works in a given situation where the derivative is not assumed to have an environmentally based advantage, it will work all the better when actually given such an advantage. However, the important finding of our study was that stabilization could occur even when no such advantage was assumed. There is no need to assume the existence of "an ecologically novel (and initially empty) habitat" as Coyne and Orr (2006: 341) imply.
There are statements in Buerkle et al. (2000) that may have caused Mavárez et al. (2006) and Coyne and Orr (2004) to misunderstand the predictions of theory as they are expressed in our paper (i.e., in McCarthy et al. 1995). Buerkle et al. (2000: 443) say the McCarthy et al. model "described conditions that favour a special case of recombinational speciation [i.e., of the process of stabilization of a new recombinant derivative derived from interchromoset matings], one in which a novel species is generated but both parental species become locally extinct" and that our model predicts a "complete genetic merger" of the parental populations. They go on to say that in most cases where such processes have been documented "the parental types continue to coexist with the derived hybrid species." Gross and Rieseberg (2005: 243) make a similar statement. Coyne and Orr cite Buerkle et al. (2000) to make the statement that "with weak ecological selection, hybrid speciation almost never occurred, while with strong ecological selection it occurred in 20% of simulation runs. Most important, in all cases the novel hybrid genotype was successfully established—and persisted for many generations—without extinction of either parental species." These are distortions of our findings. The implication is that the process as modeled by McCarthy et al. is a rare, special case, and that their own version of the model (which is actually a special case of our original model) better represents naturally occurring processes.
However, in order to focus on the early stages of the process, McCarthy et al. modeled only a very small portion of the interface region between two hybridizing populations, the region where the new recombinant derivative first arises. We were only interested in evaluating whether a recombinant derivative derived from interchromoset mating could get established in a small area within a hybrid zone. We did not evaluate how far or under what circumstances it would spread to other regions. Thus, it is true that the new recombinant derivatives in our model typically displaced the parental types. It also true, however, that our results, based on the tiny space that we modeled, in no way imply that the parental forms are driven to extinction elsewhere.
Referring to our model, Rieseberg (1997: 368) says "it seems unlikely that the hybrid genotypes would be more fit than the parentals in all habitats in the hybrid zone." Such an assumption would seem unlikely indeed—if we had made it. But we didn't. Rieseberg apparently misunderstood our model. We only assumed hybrids were at an advantage within the small portion of the zone being modeled. Moreover we only assumed one particular recombinant derivative was at an advantage, not all hybrid types that could be derived from the cross. Indeed, when we included in our simulations regions (within the small portion of the zone being modeled) where the new recombinant derivative was at a disadvantage versus the parental types, the derivative did not spread into those regions. But we did not publish these results since we deemed them self-evident. We merely wanted to see whether recombinant derivatives of interchromoset matings could get established and, if so, to investigate what factors were conducive to them doing so. To get established a new recombinant derivative has to occupy an initial limited territory.
Buerkle et al. (2000) do differ somewhat from McCarthy et al. (1995) with respect to the particulars they claim to be conducive to the this process. Nevertheless, they reach conclusions similar to those already reached in McCarthy et al. with regard to the general feasibility of the process. Thus, they (ibid: 450) note that the model can indeed lead to the production of a new stable recombinant derivative reproductively isolated from its parental forms. In fact, in McCarthy et al. the recombinant derivative is always reproductively isolated (at least partially so) because, in matings with both parental types, it produces structurally heterozygous hybrids of reduced fertility.
Neither of the two most cited theoretical papers on the topic (Buerkle 2000 and McCarthy et al. 1995) make any theoretical prediction that this process is rare. Nor do they suggest that "reproductive isolation between hybrids and their parents is difficult to achieve." In fact, the prediction made in our study is quite the contrary. There are additional misunderstandings of our model. For example, Coyne and Orr (2004) state that recombinational stabilization "is more likely if it is fast: if stabilization of a recombinant genotype that is also reproductively isolated from both parentals required, say, a thousand generations, speciation would probably not occur." This claim is inconsistent with the actual mathematics associated with the stabilization of recombinant derivatives. Thus, suppose p is the probability that the stabilization of recombinant derivative begins in any particular generation X. Further call such a beginning the "initiation of a transition." Then X, the number of generations to the initiation of a transition, is a geometric random variable with mean E(X) = 1/p. And the probability that k generations will be needed to initiate one transition is
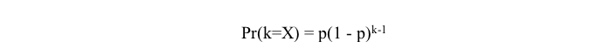
|
In the quotation above, Coyne and Orr say that if stabilization of a recombinant derivative took "a thousand generations, speciation would probably not occur." However, if the mean expectation of the time to transition were 1000 generations, we would have E(X) = 1/p = 1000, which implies that p = .001. The probability that k generations or less would be needed to initiate a transition would therefore be
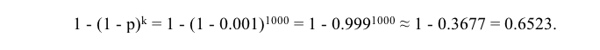
|
In other words, if the expected time required to initiate a transition were 1000 generations, then such a transition would be more likely than not to initiate sometime during the first 1,000 generations. The actual probability would be 0.6523. So the probability that initiation would occur sometime subsequent to 1,000 generations would be 0.3477. Note, too, that as k approaches infinity, 1 - (1 - p)k approaches one. This is true for any value of p such that 0 < p ≤ 1. Therefore, from the standpoint of probability theory, the initiation of a transition becomes a mathematical certainty as the number of generations increases without bound. In ordinary language then, given the passage of a very large number of generations, we expect a transition to initiate even when the probability of its initiation in any given generation is very small. So Coyne and Orr's assertion is mistaken.
Finally, it should be mentioned that certain authors (Rieseberg 1997; Coyne and Orr 2004: 350) have suggested our theoretical study (McCarthy 1995; McCarthy et al. 1995) showed inbreeding was somehow essential to stabilization of the recombinant derivative and that selfing was essential. Granted, all other things being equal, the model suggested a higher selfing rate increased the probability of producing a stable derivative, but this is the effect of only one variable (selfing rate), when all other relevant variables are held constant. True, all other things being equal, high selfing rates among the hybrids make the production of recombinant derivatives much more likely. However, since (1) outcrossing is a heritable trait, and (2) hybridization cannot occur in the absence of outcrossing, one does not expect most hybrid populations to have high selfing rates. Therefore, since most hybrid populations will be composed of outcrossers, one expects many recombinant derivatives also to be outcrossers.
Moreover, in McCarthy et al. (1995) Figure 5 indicates that transitions do occur (after many generations) when the selfing rate, s = 0, that is when outcrossing is obligate. The graph indicates this for a fitness advantage of α= 2.0 (transitions also occurred for lower values of α, but this is not indicated due to vertical truncation of the graph). In general, the results can be interpreted as indicating that in a strictly outcrossing population transitions will occur, but at rare. This is true whether the advantage of the recombinant derivative over the parental types is marked or not (only when the advantage is more marked transitions will occur less rarely). This finding should not be interpreted as a conclusion that outcrossing recombinant derivatives should be rarer than selfing ones. Instead, it should be seen for what it is: our computer simulations produced a pattern where there are typically long periods of stability punctuated by rare events where a new type suddenly appears. This model therefore provides a genetic explanation of the pervasive pattern seen in the fossil record itself where the typical fossil form is stable for millions of years and the advents of new forms are sudden, very rare events.